inm[12]=t[2] .Ьв[12] ;%можно и t[l].as[12] - их знак одинаков%

nim[ll. .1]=р[2] .yytll. .1]; Else

inm[12]-t[2] .bs[12] ;%ножно и t[l].as[12] - их знак одинаков%

inm[ll. .5]=q[2] .eum[6. .0] ;

1шв[4- l]=t[2] .be[4. .1] ;%можно и

t[l].ae[4..1]%

End If; End If;

eg.net[12. .1]=11ш>[12. .1]; zztl6..l]=sg.out[16..1];

ZI12. .l] nimI12. .1] ; END

5.7. ПОСТРОЕНИЕ БЫСТРОДЕЙСТВУЮЩИХ ПЕРЕМНОЖИТЕЛЕЙ

Реализация операции умножения аппаратными методами всегда являлась сложной задачей при разработке высокопроизводительных вычислителей Аппаратная реализация алгоритма умножения в первую очередь предназначена для получения максимальной скорости выполнения зтой операции в устройстве На ПЛИС можно разрабатывать умножители с быстродействием более 100 МГц и располагать более 100 модулей умножителей в одном кристалле

Для операндов небольшой разрядности (4 и менее) наиболее результативна структура простого матричного суммирования (Рис. 5.17) Она реализует параллельный умножитель как массив одноразрядных сумматоров, соединенных локальными межсоединениями, при этом общее число сумматоров напрямую определяется разрядностью множимого и множителя

Рис. 5.17. Структура матричного умножиталя с последоаательным распространением пареноса

одноразрядный сумматор

У! о Х2У1 хзуо х,у, хгуо хоУ1 х,уо Уо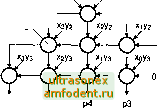

р7 р6 р5

р1 рО

Так, полный параллельный умножитель 4x4 требует для своей реализации 12 сумматоров При дальнейшем наращивании разрядности матрица одноразрядных сумматоров значительно разрастается, одновременно увеличивается критический путь, и реализация умножителя становится нерациональной

Одним из способов уменьшения аппаратных затрат служит использование алгоритма Бута В соответствии с данным алгоритмом определенным образом анализируются парные биты множителя и в зависимости от их комбинации над множимым выполняются некоторые преобразования (пример для умножителя 12x12 бит приведен в Таблице 5.3)

Таблица 5.3. Преобразование множимого в зависимости от состояния множителя

Как видно из таблицы, выполняемые над множимым действия отличаются для двух старших бит, один из которых знаковый Подобная коррекция позволяет осуществлять операцию умножения над числами в дополнительном коде

Сформированные частичные произведения, представляющие собой результат преобразования множимого, необходимо суммировать с соответствующим весовым фактором Результатом их суммирования по алгоритму простого матричного умножителя и будет конечный продукт произведения двух операндов Анализ различных методов свертки частичных произведений показал, что наиболее приемлемым для реализации на ПЛИС является алгоритм на основе иерархического дерева многоразрядных масштабирующих сумматоров При этом достигается сокращение аппаратных затрат по сравнению с параллельным матричным умножителем до двух раз

Пример реализации данного решения для случая 12-разрядных операндов приведен на Рис. 5.18 В данной схеме выбор соответствующего преобразования множимого Y осуществляется мультиплексором на основании анализа парных бит множителя X в соответствии с Таблицей 5.3 Входные значения мультиплексоров О и Y подаются непосредственно, значение 2Y формируется сдвигом множимого на один бит, а 3Y формируется путем сложения Y и 2Y

Сумматоры ADD осуществляют суммирование частичных произведений, причем их разрядность для разных ступеней иерархии неодинакова На каждом шаге суммирования, как видно, имеются несколько сквозных бит, непосредственно дополняющих выходные значения сумматоров. За счет них и за счет битов расширения знака осуществляется необходимое масштабирование результата Размерность произведения Р в конечном итоге равна сумме размерностей операндов

За счет регулярности приведенной структуры быстродействие можно резко повысить путем введения конвейеризации каждой ступени При этом разделяются конвейерными регистрами как сумматоры, так и мультиплексоры Выигрыш в быстродействии, благодаря данному решению, оказывается особенно ощутимым для большой разрядности операндов

Рис. 5.18. Структурная схема 12-разряАНого умножителя на основе алгоритма Бута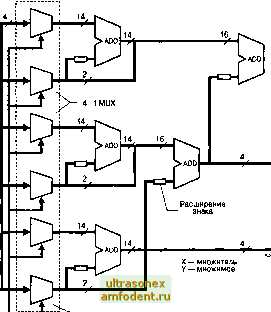

16,24,

Р[23 0]

Дешифратор Бута

Для иллюстрации метода умножения на константу рассмотрим, как выполняется умножение двух десятичных чисел в столбик на примере 85x37:

Таблица произведений множимого записывается во фрагмент памяти на ПЛИС и называется таблицей перекодировок (ТП) ТП адресуются четырьмя разрядами, следовательно, необходимо представить операнды в шестнадцатеричном коде, и массив ТП будет содержать, таким образом, массив произведений константы на ряд цифр О, 1,.. , Е, Р

Как видно из примера, используется каждая цифра множителя для поразрядного перемножения со всеми цифрами множимого и совсем необязательно знать всю таблицу произведений операндов полной разрядности. Для перемножения двух переменных достаточно иметь таблицу произведений множимого, в данном случае константы, на весь ранг возможных цифр множителя, и осуществить корректное суммирование полученных частичных произведений. Для случая 85 х 476 это иллюстрируется следующим образом

Как видно из приведенного примера, для того чтобы осуществить операцию умножения двух двенадцатиразрядных двоичных чисел, одно из которых - константа, необходимо иметь ТП на 16 значений с разрядностью выходного значения 16 (для положительных чисел) и два 16-раэрядныхсумматора- Рио. 5.19.

Четыре младших бита выходного произведения нижней на Рис. 5.19 ТП непосредственно в соответствии с алгоритмом функционирования формируют четыре младших разряда окончательного произведения

При подаче на сумматор указанного произведения необходимо произвести расширение знака в соответствии со значением старшего бита. Например, для 12-разрядных операндов: Младшее произведение (х 1) 11111110 01101101

J Сквсзнов суыымроввт

Старшее произведение (х 16) Результат

+ 0010 11010011 0010 1011 1001 1101

Реализация по данному принципу операции умножения отрицательных чисел, представленных в дополнительном коде, не требует каких-либо изменений в технической реализации и не задействует дополнительную специальную логику коррекции; изменится лишь прошивка просмотровой таблицы, адресуемой знаковым битом входного операнда.

Рис 5.19.12-разрядный умисжиталь на константу

>ADD

LOOK-UP

>ADD

LOOK-UP