Пример 32. На выходе согласованного аттенюатора действует напряжение 10 мВ при входном напряжении 200 мВ. Определите коэффициент ослабления сигнала в децибелах (дБ).

Согласно определению

- К = 201g

201g

К = -26 дБ.

10 200

201gO,05;

Пример 3.3. Коэффициент усиления по мощности усилителя равен 33 Вычислите выходную мощность, если входная мощность составляет 20 мВт.

Подставляя числовые значения в формулу

= lOlg -

получаем

Рис. 3.6. ЛС-цепочка

Рис. 3.7. ЛС-цепочка: конденсатор С заряжается через резистор R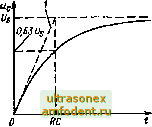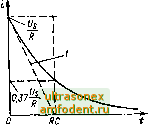

33 = lOlg

20 Р

= 2000;

вых =40-10 мВт = 40 Вт.

Рис. 3.8. Временная зависимость изменения напряжения конденсатора на рис. 3.7:

I - начальная скорость изменения напряжения URC, В/с

Рис. 3.9- Временная зависимость изменения тока конденсатора на рис. 3.7:

1 - начальная скорость изменения TOKaf/ЛС, А/с

Небольшие замечания и советы

Любой фиксированный коэффициент деления сигнала можно получить путем последовательного соединения аттенюаторов. Результирующий коэффициент деления равен произведению коэффициентов деления составляющих аттенюаторов или их сумме, если они выражены в децибелах. Например, результирующая величина, равная -19 дБ, получается при последовательном соединении аттенюаторов с коэффициентами соответственно -3, -6 и -10 дБ.

Для получения точных широкополосных аттенюаторов следует использовать точные угольные или металлопленочные резисторы. Для этого нельзя применять проволочные резисторы, так как они имеют зна чительную индуктивность.

Особое внимание следует уделять конструированию высокочастотных и сильно ослабляющих аттенюаторов. Как правило, отдельные секции многосекционного аттенюатора экранируют, тщательно разносят входные и выходные вводы, минимизируют длины соединительных

проводов, применяют высококачестветые экранированные кабели и размешают аттенюаторы в металлическом заземленном корпусе.

ЛС-цепи

ЛС-цепи очень широко используются в электронной схемотехнике в качестве времязадающих элементов. Простейшая ЛС-цепь показана на рис. 3.6. Если к ее входным зажимам подсоединить источник постоянного напряжения Ug (рис. 3.7) , то первоначально незаряженный конденсатор С начнет заряжаться.

При этом напряжение Щ между его обкладками будет экспоненциально расти, как показано на рис. 3.8. Одновременно будет экспоненциально уменьшаться ток j в рассматриваемой цепи (рис. 3.9). Скорость изменения напряжения и тока определяется постоянной времени г = CR. Причем емкость С измеряется в фарадах, сопротивление R - в омах, а постоянная времени т - в секундах.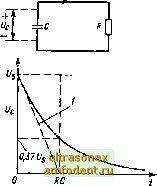

Рис. 3.10 ЛС-цсиочка: конденсатор С заряжаетсячерс i резистор Л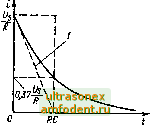

Рис. 3.11. Временная зависимость изменения напряжения конденсатора на рис. 3.10:

J - начальная скорость изменения напряжения U/RC, В/с

Рис. 3.12. Временная зависимость изменения тока конденсатора на рис. 3.10.

/ - начальная скорость изменения тока -tRC, В/с

Закон изменения напряжения на конденсаторе имеет следующий вид. где t - время, с.

В течение начального временного интервала t = т напряжение на конденсаторе воэрастаег до 0,63 U. За следующий такой же временной интервал напряжение изменится на 0,63 (Ug - 0,63 Ug) и т.д.

Теоретически конденсатор никогда не зарядится до максимального напряжения, равного Ug. Однако за время порядка 5 т напряжение на нем столь незначительно отличается от Щ, что процесс заряда можно считать закончившимся и принять Uq = Ug.

Заряжетый конденсатор запасает энергию в виде электрического поля. Если полностью заряженный конденсатор включить в схему, приведенную на рис. 3.10, то он начнет разряжаться через резистор и напряжение между его обкладками будет уменьшаться так, как показано на рис. 3.11. На рис. 3.12 приведен процесс изменешя тока в той же цепи. Скорость уменьшения тока и напряжения, как и в предыдущем случае, определяется постоянной времени т = CR. В этом случае напряжение

-tiCR

с (О

Ug.-

в предположении, что начальное напряжение на конденсаторе равно Lg. 54

В течение начального временного интервача г = т напряжение и ток ко!щенсатора уменьшатся до 037 начапьного значения. За следующий такой же временной интервал t - т напряжение и ток еще раз уменьшатся до 0,37 оставшегося значения и г.д. Теоретически конденсатор никогда полностью не разряжается, поэтому считается, что за время, примерно равное 57, напряжение и ток оказываются настолько малы, что их можно считать равными нулю.

Пример 3.4. Незаряженный конденсатор емкостью 1 мкФ подсоединяется к источнику постоянного напряжения 9 В через резистор сопротивлением 3,3 МОм. Рассчитайте напряжение на конденсаторе спустя 1 с.

Закон изменения напряжения на конденсаторе записывается в вида

где t/s = 9 В; т = СЛ = Ю * - 3,3 10* = 3,3 с; f = 1 и Поэтому

UfU) = 9(1 -е = 2.358 В.

Пример 3.5. Конденсатор емкостью 10 мкФ был сначала заряжен до напряже1Н1я 20 В, а затем разряжен через резистор сопротивлением 47 кОм. Рассчитайте время, за которое напряжение на конденсаторе уменьшится до 10 В.

Закон изменения напряжения на конденсаторе записывается в виде

- tiT

где Ug = 20 В; т = CR = 10 - Ю * -47 10 = 470 мс; UcO) = 10 В-Поэюму время

Г = Tin

= 470 In

20 10

= 470 1п2 = 470 0,693 = 325 мс.

Передача сигнала прямоугольной формы ЛС-цепью

Иа рис. 3.13 показана сглаживающая ЛС-цСпОчка, которая при определенных условиях может вьшолнять роль интегрирующего звена. На рис. 3.14 приведена RC-чегл, которая в зависимости от своих параметров может выполнять функции разделительного звена, укораадва-ющей или диф<1>ерснцирующей цепочки.

Эффекпшность рассматриваемых цепочек зависит от соотношения между постоянной времени т - RC и периодом входного сигнала t. Например, функция интегрирования выполняется тем лучше, чем сильнее выражено неравенство т> t. При этом автоматически выпoJШяcтcя

о о-

Рис. 3.13. Интегрирующая ЛС-цепочка Рис. 3.14. Дифференцирующая ЛС-цепочка

RCt RC t RC t

Рис. 3.15. Форма импупьсов напряжения на рис. 3.13

RC t

RC -t

Рис. 3.16. Форма импульсов напряжения на рис. 3.14

соотношение U t. Функция дифференцирования цепочкой, показанной на рис. 3.14, вьшолняется тем лучше, чем сильнее выражено неравенство т<1. При зтом опять-таки вх - В этом заключает-

ся очень существенный недостаток рассматриваемых схем. На рис. 3.15 и 3.16 приведены временные диаграммы U и t/ дня разных значений т. На рис. 3.16 нужно обратить внимание на положение нулевой пинии на кривых выходного сигнала U, который является чисто переменной величиной, так как конденсатор С постоянную составляющую напряжения не пропускает

Пример 3.6. Требуется спроектировать укораадвающую RC-цепъ типа данной на рис. 3.14 дпя получения последовательности коротких поло-жи1елы{ых и отрицательных импульсов. Входным сигналом является последовательность прямоугольных импульсов частотой 1 кГп с временем импульса, равным времени паузы.

В соответствии с временными диаграммами на рис. 3.16 следует выбрать постоянную времени т много меньше периода входного сигнала, т.е.

т < t.

Остановимся на т = RC = 0,1г и некотором среднем значении сопротивления резистора R, например 10 кОм. В таком случае

= 0,01.10-Ф=10пФ.

10 10

Практически для решения задачи подойдет любое значение С, равное или меньшее 10 нФ. При очень маленькой емкости (скажем, 1 нФ) длительность выходного сигнала будет крайне незначительна, а если фронт нарастания и спада входного сигнала не идеален, то И амплитуда выходного сигнала окажется весьма мала. Поэтому можно остановиться на значениях 4,7 или 2,2 нФ.

Пример 3.7. Требуется спроектировать RC-цепочку типа данной на рис. 3.13 для получения напряжения треугольной формы из входного сигнала, имеющего форму прямоугольных импульсо с длительностью импульса, равной времени паузы, и частотой 1 кГи.

В соответствии с временными диаграммами на рис. 3.15 следует выбрать постоянную времени т много больше периода входного сигнала, т.е.

т> t.

Выбирем т =ЛС = lOf.Сопротивление резистора R можно принять равным некоторому среднему значению, например 10 кОм. Тогда

= 10 * Ф = 1 мкФ.

С = -i =

10 i 10

10 - 10-

Таким образом, можно взять емкость равную или большую полученной. Правда, при слишком большой емкости (скажем, 10 мкФ) амплитуда выходного сигнала будет весьма мала. Поэтому целесообразно выбрать емкость, равную 2,2 или 4,7 мкФ.

ЛЛ-цепи

В электронной схемотехнике ЛЛ-цепи также могут использоваться для задания временнь1Х интервалов и для преобразования формы импульса. Однако катушка индуктивности чаще всего является нежелательным элементом в электронной схеме, поскольку она занимает много места, имеет большие габариты и является источником помех. Кроме того, изготовителю аппаратуры приходится нестандартные катушки изготавливать самому, что тоже крайне неудобно. Поэтому катушки не всегда удобно применять во времязадающих цепях и формирователях импульсов, хотя довольно часто их использование просто необходимо.

На рис. 3.17 приведена простейшая последовательная цепь, состоящая из индуктивности Л, резистора Л и источника постоянного напряжения. В момент подключения источника в цепи появляется ток (рис. 3.18).