Первая цифра: коричневый пояс 1; вторая цифра: черный пояс 0; множитель: красный пояс (хЮО); следовательно, номинал: 10 х 100 = = 1000 = 1 кОм; точность: золотой пояс ±5%.

Пример 23. Резистор маркирован четырьмя цветными поясами в следующей последовательности: голубой, серый, оранжевый, серябряный. Каковь[ его номинал и точность?

Первая цифра: голубой пояс 6; вторая цифра: серый пояс 8; множитель: оранжевый пояс (хЮОО); следовательно, номинал: 68 х 1000 = = 68 кОм; точность: серебряный пояс ±10 %.

Пример 2.4. Резистор маркирован четырьмя цветными поясами в следующей последовательности: оранжевый, оранжевый, серебряный, серебряный. Каковы его номинал и точность?

Первая цифра: оранжевый иояс 3; вторая цифра: оранжевый пояс 3; множитель: серебряный пояс 0,01; следовательно, номинал: 33 0,01 = = 0,33 Ом; точность: серебряный пояс ±10%.

Пример 2.5. Резистор маркирован пятью цветными поясами в следующей последовательности: красный, желтый, черный, черный, красный. Каковы его номинал и точность?

Первая цифра: красный пояс 2; вторая цифра: желтый пояс 4; третья цифра: черный пояс 0; множитель: черный пояс (х1); следовательно, номинал: 240 х 1 = 240 Ом; точность: красный пояс +2%.

Маркировка резисторов по системе BS 18S2

Некоторые типы резисторов маркируются по системе British Standart 1852. В этой системе положение децимальной запятой определяется соответствующей буквой. Другими словами, буквой определяется значение множителя (табл. 2.4).

Вторая буква в обозначении резистора определяет его точность (табл. 2.5).

Таблица 2.4. Определение множителя по системе BS 18S2

Таблица 2.5. Огфеделеяис точности по системе BS 1852

Пример 2.6. Маркировка резистора 4R7K означает 4,7 Ом ± 10%.

npHMq> 2.7. Маркировка резистора 330RG означает 330 Ом ± 2%.

Пример 2.8. Маркировка резистора R22M, означает 02 Ом ± 20%.

Поспедоватепьное и параллельное соединение резисторов

Резисторы с фиксированным значением сопротивления могут соединяться последовательно и параллельно для того, чтобы получить требуемое новое значение сопротивления. Примеры таких соединений приведены на рис. 2.4 и 2.S.

При последовательном соединении резисторов новое значение сопротивления получается как сумма составляющих:

для рнс. 2.4, в

R = R1 + R2;

для рис. 2.4j5

R =RJ +R2 +RS.

В случаях параллельного соединения резисторов суммируются обратные составляющие сопротивлений: для рнс. 2.5д

1 1 - +

r ri R2

для рис. 2.5,6

11 1 1 r ri R2 R3

RI R2

-4=1-cm-

Рис. 24. Последоветельиое соединение резисторов Рис. 2.5. Параллельное соединение резисторов

Для случая двух параллельно соединенных резисторов результирующее сопротивз1ение может быть найдено как произведение составляющих, деленное на их сумму, т.е.

Рис. 2.6. Делитель напряжения

R1 R2 R1 +R2

С помощью приложения 1 можно определить результирующее сопротивление без использования формул.

Прим) 2.9. Требуется получить сопротивление 400 кОм. При помощи какого последовательного соединения можно решить эту задачу, если отсутствует резистор, имеющий требуемый номинал?

Для этого соединим носледовательно два резистора с номинальными сопротивлениями 180 и 220 кОм и получим

R = я; + /г2 = 180 + 220 = 400 кОм.

Оба выбранных резистора входят в серию Е12. Следует отметить, что здесь не затронут вопрос о рассеиваемой мощности, однако можно определенно сказать, что на каждом из составляющих сопротивлений будет рассеиваться меньшая мощность, чем на суммарном сонротив-лении.

Прнм> 2.10. Требуется сопротивление 5 кОм мощностью 1 Вт. При помощи какого параллельного соединения можно решить эту задачу?

Два резистора сопротивлением по 10 кОм каждый, соединенные параллельно, дают суммарное сопротивление

R] R2 R1 +R2

10 10 10 -НО

= 5 кОм.

Таким образом, если параллельно соединяются два резистора, имеющие одинаковое сопротивление, то результирующее сопротивление получается вдвое меньше. Напряжение на этих резисторах одно и то же (см. рис. 2.5/2), а ток, протекающий через каждый из них, в два раза меньше суммарного тока. Поэтому мощность, рассеиваемая каждым из составляющих резисторов, оказывается также вдвое меньше суммарной мощности. Следовательно, для рассматриваемого соединения следует взять резисторы по 10 кОм мощностью 0,5 Вт.

Делитель напряжения

Резисторы часто используются в составе делителя напряжения для получения фиксированного значения напряжения (рис. 2.6). В этом случае выходное напряжение 7 связано с входным U (без учета возможного сопротивления нагрузки) следующим соотношением:

= и.

вых вх

1/?г

Пример 2.11. С помощью резисторного делителя нужно получить на нагрузке сопротивлением 100 кОм напряжение 1 В от источника постоянного напряжении 5 В.

Требуемый коэффициент деления напряжения 1/5 = 0,2. Используем делитель, схема которого приведена на рис. 2.6. Сопротивление резисторов R1 и R2 должно быть значительно меньше 100 кОм. В этом случае При расчете делителя сопротивление нагрузки можно не учитывать. Следовательно,

R1 +R2

= 02;

R2 = G,2R1 -t 0,2Я2; R1 = 4R2.

Поэтому можно выбрать R2 = 1 кОм, R1 = А кОм. Сопротивление Л7 получим путем последовательного соединения стандартных резисторов 1,8 и 2,2 кОм, выполне1шых на основе металлической пленки с точностью ±1% (мощностью 0,25 Вт). Следует помнить, что сам делитель потребляет ток от первичного исто<[Ника (в данном случае 1 мА) и этот ток дет возрастать с уменьшением сопротивлений резисторов делителя.

Небольшие замечания и советы

Для получения заданного значения напряжения следует применять высокоточные резисторы.

Недостатком простого резисторного делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение вых делителя изменяется.

;я уменьшения влияния нагрузки на {7 необходимо выбирать соротивление R2 по крайней мере в 10 раз меньше минимального сопротивления нагрузки.

Важно помнить о том, гго с уменьшением сопротивлений резисторов R1 и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1-10 мА.

Делитель тока

Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 2.7 ток /д , составляет часть общего тока 7, определяемую сопротивлениями резисторов Я7 иЯ2, т.е. можно записать, что

вых вх к}л2

Пример 2.12. Стрелка измерительного прибора отклоняется на всю шкалу в том случае, если постоянный ток в подвижной катушке равен 1 мА. Активное сопротивление обмотки катушки составляет 100 Ом. Рассчитайте сопротивление шунта так, чтобы стрелка прибора максимально отклонялась при входном токе 10 мА (см. рис. 2.8).

Коэффищ1ент деления тока определяется соотношением

вых 1 RI

- = - =0,1 = -

вх R1+R2

Отсюда

O.IRI + 0,Ш2 = R]; 0,lR] + 10 = R];

; R2 = 100 0м.

R1 =-

10 0.9

= 11,1 Ом.

Небольшие заметания и советы

Для обеспечения хорошей точности деления токов следует использовать высокоточные (±1%) резисторы.

Законы Кирхгофа

Законы Кирхгофа касаются алгебраической суммы токов или напряжений в любой электрической цепи. Когда говорят об алгебраической сумме, то имеют в виду, что токи в цепи могут иметь разные направления, а напряжения - разную полярность. Чтобы это учесть, одно из направлений принимается за положительное, а другое - за отрицательное. Соответственно одной группе токов или напряжений присваивается знак плюс (+), а другой - знак минус (-).

На рис. 2.9/г представлен закон для токов в узле: алгебраическая сумма токов в узле равна нулю. При этом считают, что токи, направленные к узлу {II, /4, /j), положительные, а токи, направленные от узла, - отрицательные (/j, /3).

На рис. 2.9,6 проиллюстрирован закон для напряжений в контуре: алгебраическая сумма напряжений в контуре равна нулю. При этом выбрано соответствующее направление обхода контура (показано стрелкой) . Если при обходе контура батарея нересекается от отрицательного полюса к положительному, то ее ЭДС записывается с положительным знаком (El), если наоборот, - с отрицательным (-е2). В правой части равенства записывается сумма напряжений иа резисторах, т.е.

е1-е2 = Ui +u2.

Требуемое сопротивление резистора R1 можно получить путем последовательного соединения двух стандартных резисторов сопротивлением 9,1 и 2 Ом, выполненных на основе юлстопленочной технологии с точностью ±2% (0,25 Вт). Заметим еще раз, что на рис. 2.8 сопротивление Л2 - это внутреннее сопротивление измерительного прибора.

Рис. 2.7. Делитель тока

\R2=100

Рис. 2.8. К примеру 2.12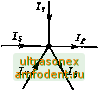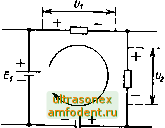

> егЕг=и%и, 5)

Рис. 2.9. Иллюстрация законов Кирхгофа:

а - сумма токов в узле равна пулю; б - сумма напряжений в замкнутом контуре равна нулю