Рис. 3.17.ЛХ.-цепочка

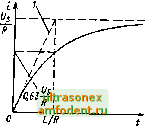Рис. 3.18. Временная диаграмма тока в индуктивности, представлешюй на рис. 3.17: / - начальная скорость изменения тока VL, А/с

Рис. 3.19. Временная зависимость изменения напряжения индуктивности, представленной на рис. 3 17:

1 - начальная скорость изменения напряже ния Ug/L, В/с

Скорость изменения тока определяется постоянной времени, равной отношению индуктивности к сопротивлению резистора, т.е.

где L - индуктивность, Гн; Л - сопротивление резистора, Ом; г-время, с.

Напряжение, приложенное к катушке Ui, изменяется во времени в соответствии с уравнением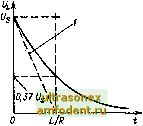

t/,e

-tiT

где T=L/R.

Эта зависимость представлена на рис. 3.19, откуда хорошо видно, что напряжение на катушке уменьшается со временем. За время, равное т, оно уменьшается до 37% начального значения Ug. Ток в цепи за это же время возрастает до максимально возможного значения 0,63 (Ug/R). За следующий временной интервал такой же длительности относительное изменение напряжения и тока будет точно таким же.

Поэтому теоретически ток в цепи и напряжение на индуктивности никогда не достигают своих предельных значений. Принято считать, что за время 5 т переходный процесс роста тока и спада напряжения практически завершается. При этом f/ считается равным нулю, а ток - равным UglR. С помощью приложения 2 можно проанализировать процессы в 1Л-цепи, не прибегая к помощи формул.

Во время протекания тока через катушку в ней накапливается энергия, заключенная в электромагнитном поле. При изменении тока должна меняться и энергия. EaiH сохраняется замкнутая электрическая цепь, то лишняя энергия рассеивается в виде тепла в резисторе. Если электрическая цепь внезапно разрывается, то на катуипсе возникают значительной амплитуды всплески напряжения (противоЭДС), за счет которых индуктивность стремится поддержать протекание прежнего тока в том же направлении. Алвшитуда возникающего импульса напряжения, прямо пропорциональная индуктивности катушки L и скорости обрыва тока, записывается в виде

е = L - . dt

Знак производной от тока по времени (положительный и отрицательный) зависит от того, растет ток или уменьшается.

Пример 3.8. Через катушку, имеющую индуктивность 100 мГн, течет ток 10 мА, который отключается электронным ключом за 20 мкс. Определите возникающую на зажимах катушки противоЭДС.

Скорость изменения тока катушки

di dt

10 10 20 10

= -0,5 . 10 А/с.

Генерируемая противоЭДС

е = Л - = 100 10 dt

(-0,5 - 10) = -50 В.

Таким образом, на зажимах катушки возникает импульс напряжения с амплитудой 50 В. Время его спада определяется конкретной схемой включения катушки.

Передача сигнала прямоугольной формы ЛЛ-цепью

Цепи, показанные на рис. 3.20 и 3.21, могут вьтолнять те же функции, что и ранее рассмотренные ЛС-иепи. Так, схема на рис. 3.20 сглаживает импульсный входной сигнал и при условии tbix Ч)х вьшолняетоперацию его интегрирования, если постоянная времени L/R много больше периода частоты входного сигнала. На рис. 3.22 приведены соответствующие временные диаграммы входного и выходного сигналов.

Рис. 3.20. /?i-HiiTerpMpyramaH цепочка Рис. 3.21. Л/.-диффсрсицирующая цепочка

L/R-t

L/R i

L/R f

Рис. 3.22. Импульсы напряжения /?i-ueno4KH, представленной на рис. 3.20

L/Ri

L/R t

L/R t

Рис- 3.23- Импульсы напряжения jRi4icno4KM, представленной на рис. 3.21

Схема, показанная на рис 3.21, при условии U < j/x, которое выполняется при L/R<t, осуществляет операдаю дифференцирования входного сигнала. Соответствующие временные диаграммы приведены на рис. 3.23.

Однако стоит отметить, что на практике для вьшолнения описанных операций всегда используются ЛС-цепи. Поэтому здесь не рассмотрены примеры использования RL -цепей.

Накопление энергии

Конденсаторы и катушки индуктивности способны накапливать электрическую энергию. Конденсатором она запасается в электрическом поле и определяется следуюишм уравнением:

Е = - си , 2

где С - емкость, Ф; U-напряжение. В; Е - энергия, Дж.

Катушкой индуктивности энергия запасается в магнитном поле и определяется соотношением

Рис. 3.24. Последовательный резонансный £С-контур

Е = 0,5,/

Рис. 3.25. Параллелы1Ый колебательный iC-KoiiTyp

где i - индуктивность, Гн; / -ток. А; £-энергия, Дж.

Типичным примером накопителя энергии в электронной схеме является конденсатор сглаживающего фильтра вьшрямите:1я. Этот резервуар энергии периодически подзаряжается от ганающей сети через выпрямитель переменного тока. В течение временных интервачов, когда выпрямитель находится в непроводящем состоянии, вся схема потребляет необходимую энергию непосредственно из конденсатора (он разряжается через нагрузку).

Если напряжение в питающей сети переменного тока внезапно пропадает, то конденсатор может в течение нескольких десятков периодов частоты питающей сети поддерживать функционирование электронной схемы за счет имеющихся в нем запасов энергии

ЛС-цепи

На рис. 3.24 представлена последовательная резонансная £.Сцепь, а на рис. 3.25 - параллельная iC-цепь. Сопротивление этих цепей переменному току сильно зависит от частоты сигнала. Для схемы на рис. 3.24 справедливо соотношение

где Z - сопротивление последовательной цепи. Ом; Х/ и Х(- - сопротивления катушки и конденсатора соответственно, Ом.

Фазовый сдвиг между питающим схему переменным напряжением и током равен +я/2 рад (или +90°), когда Xi > Хс (на частоте вьиие резонансной), или -я/2 рад (или -90°), когда Х < Хс (на частоте ниже резонансной). На частоте последовательного резонанса ЛГ - ч полное сопротивление контура равно нулю. Ток при этом максимален.

Сопротивление параллельного контура (цепи), показанного на рис. 3.25, определяется соотношением

Рис. 3.26. Последовательный tC/J-контур

Рис. 3.27. Параллельный Z,CT-KOHTyp

Фазовый угол между питающим напряжением и током контура равен + 7г/2 рад (или +90°) , если Xi > Хс (на частоте выше резонансной) , или -7г/2 (или -90°) , если Xi < Х (на частоте ниже резонансной) .

На частоте параллельного резонанса \Xi\ = .Ус1>п°этому полное сопротивление контура Z неограниченно возрастает. При этих условиях ток контура будет минимален (в идеальном случае он равен нулю) .

LCR-UfxiH

Во всех реальных ЛС-цепях всегда присутствует активное сопротивление. Это может быть сопротивление обмотки катушки, сопротивление утечки ковденсатора, сопротивление нагрузки и т.д. В целом ряде случаев необходимо учитывать влияние этого сопротивления на свойства цепи. На рис. 3.26 и 3.27 показаны соответственно носледовательный и параллельный LC-контуры. Результирующее сопротивление каждого контура зависит от частоты.

Для схемы на рис. 3.26 можно записать

Z = s/R + (А- - ХУ.

На частоте резонанса 11 = 1! ц Z = R.

Фазовый сдвиг входного напряжения относительно общего тока

Ф = arctg

Результирующее сопротивление контура на рис. 3.27 вычисляется в виде

На частоте параллельного резонанса \Xj\ - \Хс\ н Z = R. Фазовый сдвиг между током и напряжением

Ф = arctg

RiX, - Х )

Резонанс

Частота, на которой сопротивление последовательного LC-контура равняется нулю, а параллельного - неограниченно возрастает, называется резонансной. В обоих случаях резонансная частота

где L - индуктивность, Гн; С - емкость, Ф; /о - частота, Гц.

Зависимости сопротивления от частоты для обеих схем показаны на рис. 3.28 и 3.29. В каждом случае на резонансной частоте /о результирующее сопротивление контура равно R. Характеристика типа данной на рис. 3.28 называется резонансной, а на рис. 3.29 - режекторной (заградительной) .

Качество резонансной и режекторной цепей определяется их добротностью Q. Чем больше добротность, тем более острой будет характеристика, и наоборот: чем меньше добротность, тем более пологой выглядит характеристика. В случае последовательного контура добротность увеличивается при уменьшении Л, а в случае параллельного контура она увеличивается при увеличении R.

Таким образом, вид характеристики можно менять путем введения в контур соответствующего сопротивления. Полоса пропускания контура определяется уравнением

Пример 3.9. Резонансная частота параллельного АС-контура равна 400 Гц. Индуктивность катушки 400 мГн. Необходимо рассчитать емкость конденсатора. Из выражения для резонансной частоты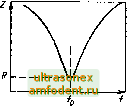

Рис. 3.28. Зависимость сопротивления от частоты послецоватслыюго резонансного контура

Рис. 3.29. Зависимость сопротивления от частоты параллельного резонансного контура