где [х и [Хр - соответственно подвижности электронов и дырок. Поскольку напряжение в /-области Vi=2dE, после совместного решения уравнений (2.35) и (2.36) имеем

Vi=-iM!-. (2.37)

Это выражение дает очень ценную информацию о двух основных факторах падения напряжения на р-/-п-диодах и тиристорах в открытом состоянии. Напряжение Vi обратно пропорционально эффективному времени жизни и прямо пропорционально квадрату ширины базы прибора. Это отражает основные тенденции, встречающиеся в реальных приборах, и объясняет важность минимизации ширины базы тиристора при обеспечении высокого времени жизни.

Дальнейшее понимание сущности физических процессов, влияющих на напряжение тиристора в открытом состоянии, может быть получено, если использовать понятие коэффициента ламби-полярной диффузии

Da=--, (2.38)

где Dp= (/гГ/)/р,р - коэффициент диффузии дырок; D = = (kT/q) р , - коэффициент диффузии электронов. Поскольку при высоких уровнях инжекции п=р, то

Dn/Dp = iin/li-p = b,

и выражение (2.37) принимает следующий вид:

Совершенно ясно, что напряжение Vi также уменьшается обратно пропорционально амбиполярному коэффициенту диффузии. В свою очередь, этот параметр сильно зависит от концентрации электронов, если она превышает 10 cм~ что обусловливается взаимодействием между подвижными носителями или так называемым рассеянием носителей на носителях. Зависимость между коэффициентом амбиполярной диффузии и концентрацией электронов показана на рис. 2.23.

Эффективное время жизни также зависит от концентрации электронов. При низких уровнях инжекции оно равно сумме времен жизни неосновных носителей, электронов и дырок [Sze, 1981] или амбиполярному времени жизни Ха, т. е.

Tell = Xa = XpO-\-XnO- (2.40)

В условиях высокой инжекции время жизни ограничивается оже-рекомбинационными эффектами [Nilsson, 1973]. Рекомбина-ционный процесс заключается в том, что электрон и дырка могут

п, электронов/см

Рис. 2.23. Зависимость коэффициента амбиполярной диффузии от концентрации электронов (Chandi, 1977]

ю г S 10 2 5 10 г

п, электрон/см

Рис. 2.24. Зависимость эффективного времени жизии от концентрации электронов [Chandi, 1977]: 1-т при С = 2,9.10-- cmVc

непосредственно рекомбинировать и при этом сообщать энергию любому другому электрону или дырке. В этом случае эффективное время жизни задается в виде

- =- + -- (2.41)

Tell Ха Ха

Здесь ха = 1/СаП, где -скорость оже-рекомбинации (для кремния G 2,9-10~ cmVc) [Nilsson, 1973]. Вышеприведенное уравнение представлено графически на рис. 2.24. Что касается коэффициента амбиполярной диффузии, то эффекты высокой инжекции начинают доминировать при концентрации электронов выше 10 см~. Когда плотность тока, а следовательно, и концентрация носителей начинают увеличиваться, эффективное время жизни резко уменьшается, и с учетом уравнения (2.39) можно вычислить скорость падения напряжения.

В вышеприведенном упрощенном рассмотрении р-i-п-диода были игнорированы два фактора, которые имеют важное влияние на падение напряжения тиристора в открытом состоянии. Речь идет о падении напряжения на крайних областях и эффективности инжекции эмиттеров. Эти эффекты учитываются в более сложных теориях [Hall, 1952], [Herlet, 1968] решения уравнений переноса и непрерывности носителей. Была получена следующая зависимость между током и напряжением, приложенным к прибору;

-f,. p(f)- (2-42)

I==2qniDud-

Здесь - это сложная функция, зависящая от падения напряжения в базовой области прибора; d - половина ширины базы;

Зависимость функции f, от d/La для кремния приведена на рис. 2.25. Здесь Lo= (D To) - длина амбиполярной диффузии. Заметим, что функция имеет максимальное значение при d/La = = 1, если прямое падение напряжения в этой точке минимально.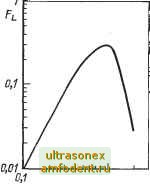

1,0 d/La

Рис. 2.25. Зависимость функции от ct/La для р-I-п-диода

В [Choo, 1970] исследовалось влияние времени жизни (или Lo) на падение напряжения диода, включая эффекты рекомбинации в крайних областях.

На практике прямое напряжение снижается с увеличением времени жизни носителей до тех пор, пока d/Lal. При высоком времени жизни напряжение снижается очень медленно или даже остается постоянным.

Это можно объяснить, если допустить отсутствие рекомбинации в крайних областях. Увеличение напряжения, обусловленное носителями, заполняющими крайние области, компенсирует уменьщение падения напряжения в базе при увеличении времени жизни. Однако при рекомбинации в крайних областях эти носители подавляются и напряжение монотонно уменьшается с увеличением времени жизни. Расчеты IOкaзaли, что дальнейщее увеличение времени жизни незначительно влияет на падение напряжения.

2.4.2. Модели тиристора в открытом состоянии

Рассмотрим сначала аналитическую модель, предложенную в [Otsuka, 1967], с учетом ряда упрощающих и аппроксимирующих допущений для того, чтобы определить падение напряжения в прямом проводящем состоянии тиристора. Структура тиристора показана на рис. 2.26.

Диффузионные длины неосновных носителей заряда в областях N2, Р2 -и Р1 всегда превышают ширину этих областей, но для базы Л(/ справедливо обратное утверждение. Концентрации примеси в областях РО и N2 одинаковы, а кроме того, W2 = ро-Концентрация в области Р1 равна концентрации в области Р2.

Катод < N2

1А/Я2

PD Анод

Vnz pz Щ1 pz Уро

Рис. 2.26. Моделируемая структура тиристора в открытом состоянии